Please refer to the new version of this article for some revisions.
The nuclear norm has been on the spotlight of optimization for quite a while, largely due to the breakthrough work of Emmanuel Candeson exact matrix completion and recovery years back. Summing up the singular values, this norm can be considered as the 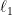 norm in the spectral domain, reminiscent of the intriguing relationship between the
norm in the spectral domain, reminiscent of the intriguing relationship between the  (quasi)norm and the
(quasi)norm and the 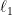 norm, revealed in compressive sensing. In fact, this norm best approximates the rank for a given matrix under some technical conditions (aka. serving as the convex surrogate). To be precise, for a particular matrix
norm, revealed in compressive sensing. In fact, this norm best approximates the rank for a given matrix under some technical conditions (aka. serving as the convex surrogate). To be precise, for a particular matrix 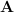 , its nuclear norm is defined as
, its nuclear norm is defined as  , where
, where 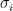 denotes the
denotes the 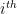 singular value (henceforth assuming singular values sorted in descending order). Then
singular value (henceforth assuming singular values sorted in descending order). Then  is the best under-estimator (technically the convex envelope) of
is the best under-estimator (technically the convex envelope) of  over the domain
over the domain  , where
, where  is the spectral norm or equivalently the largest singular value
is the spectral norm or equivalently the largest singular value 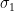 . The last condition on the spectral norm is in fact trivial, as one can always scale the matrix to make
. The last condition on the spectral norm is in fact trivial, as one can always scale the matrix to make 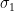 valid (in practical optimization, this possibly entails adjusting of parameters).
valid (in practical optimization, this possibly entails adjusting of parameters).
Most nuclear norm related (convex) optimization can be recast as SemiDefinite Programming problems, due to the simple variational characterization of the nuclear norm (see Proposition 2.1 in this paper)

Despite the elegance, this approach is numerically unwise as most interior-point solvers can only handle problems up to hundreds of variables both for hardware and algorithmic reasons. On the other hand, most current applications such as large-scale matrix completion and the Robust PCA (by Cand\`{e}s et al) have been numerically feasible due to the closed-form solutions to some canonical forms of nuclear norm optimization (most popular and foremost the singular value thresholding (SVT) operator). These line of results has served as the key to success of recent numerical schemes such as the accelerated proximal gradient (APG) and the augmented Lagragian multiplier(ALM) methods , for nuclear norm optimization. Hence discovery and hopefully systematic investigation into such closed-form solutions are both necessary and interesting in their own right.
— 1. Realizing the importance of unitarily invariant property (UIP) —
My recent investigation into the low rank representation for subspace segmentation (ref. my earlier post here and this paper) has boiled down to understanding this problem

and it turns out
Theorem 1 The minimizer  to problem (2)obeys
to problem (2)obeys  , where
, where  is the singular value decomposition of
is the singular value decomposition of  . Moreover,
. Moreover,  is also the minimizer to this problem:
is also the minimizer to this problem:

While these results bear some direct links with what comes later, they have provided us with important clues to investigate the above closed-form problem. There it is. When trying to model practical data points contaminated with outliers, we consider this model

And numerical tackle to this model involves the subproblem

To establish the closed-form solution to this problem, it turns out the unitarily invariant property of the nuclear norm is critical.
Definition 2 (Unitarily Invariant Norms) For  , and unitarily matrices
, and unitarily matrices  and
and 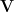 (aka.
(aka.  , and similar for
, and similar for 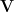 ). A norm
). A norm  is unitarily invariant if and only if
is unitarily invariant if and only if  for any
for any  and
and 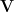 . (
. ( here denotes conjugate transpose over the complex matrix field)
here denotes conjugate transpose over the complex matrix field)
Two families of unitarily invariant norms are particularly relevant here. One is the Schattern 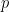 norms defined as
norms defined as  (assuming
(assuming  ); the other is the Ky-Fan
); the other is the Ky-Fan  norms, defined as
norms, defined as  (assuming descending order of singular values). Clearly the nuclear norm is the Schatten
(assuming descending order of singular values). Clearly the nuclear norm is the Schatten  norm (or Ky-Fan
norm (or Ky-Fan  norm), and hence unitarily invariant. Similarly the Frobenius norm is the Schatten
norm), and hence unitarily invariant. Similarly the Frobenius norm is the Schatten  norm and hence also enjoys the nice property.
norm and hence also enjoys the nice property.
— 2. Deriving closed-form solutions of nuclear norm problems by unitarily invariant property —
I have progressively realized the UIP can be used for figuring out closed form solutions to several canonical forms of nuclear norm optimization problem. Though results presented below are known from various authors, I don’t like their proofs in general because their proofs are by construction in nature — it is beautiful but not generalizable nor stimulating, esp. to complicated forms and further problems.
Before the exposition, I’d like to briefly review some facts from convex analysis and optimization (ref. Boyd and Vandenberghe). A real-valued function  is convex if and only if its domain
is convex if and only if its domain  is a convex set and
is a convex set and  for
for  and
and  (the description can be considerably simplified with the extended-value extensions); it’s strictly convex if and only if the inequality always holds strictly. Now consider minimizing a convex function
(the description can be considerably simplified with the extended-value extensions); it’s strictly convex if and only if the inequality always holds strictly. Now consider minimizing a convex function  in practice, or generically
in practice, or generically

where 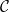 is the convex domain that’s dictated by constraints. Suppose
is the convex domain that’s dictated by constraints. Suppose 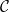 is nonempty, aka. the problem is feasible, then
is nonempty, aka. the problem is feasible, then
Lemma 3 (Convexity and Uniqueness of Minimizers) For the generic convex optimization (6)with a nonempty domain 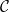 , we have
, we have
- 1) For the additive composite function
 ,
,  with convex components,
with convex components,  ,
,  is strictly convex so long as any component function is strictly convex.
is strictly convex so long as any component function is strictly convex.
- 2) If
 is strictly convex, the minimizer to (6) is always unique.
is strictly convex, the minimizer to (6) is always unique.
- 3) When
 is not strictly convex, the minimizer(s) to (6) may or may not be unique.
is not strictly convex, the minimizer(s) to (6) may or may not be unique.
The first and second can be easily verified from first principle of strict convexity, while the third can be loosely cemented with examples, esp on why strict convexity is not a necessary condition for the uniqueness. Take  for example. The objective is obviously not strictly convex (in fact, local linearity is a typical kind of antidote for thus), but the minimizer is only the origin (it looks as if it was strictly convex in the
for example. The objective is obviously not strictly convex (in fact, local linearity is a typical kind of antidote for thus), but the minimizer is only the origin (it looks as if it was strictly convex in the  vicinity of the origin). There are numerous reasons for which such unicity can arise and I won’t push towards enumerating them; instead, I’d like to note that a useful technique to prove such unicty is by perturbation analysis: for a candidate minimizer of (6), say
vicinity of the origin). There are numerous reasons for which such unicity can arise and I won’t push towards enumerating them; instead, I’d like to note that a useful technique to prove such unicty is by perturbation analysis: for a candidate minimizer of (6), say  , it is the unique minimizer if and only if
, it is the unique minimizer if and only if  where
where  . This is justified since for convex functions, any local minimizer is also a global minimizer while the convexity of domain suggests such minimizers must be spatially contiguous.
. This is justified since for convex functions, any local minimizer is also a global minimizer while the convexity of domain suggests such minimizers must be spatially contiguous.
Now I’ll close the loop by presenting the UIP version of sketchy proofs to several known results on nuclear norm.
Theorem 4 (Singular Value Thresholding and EigenValue Thresholding)We have the following analytic results
Proof: 1) (7) is strongly convex and hence has a unique minimizer. It is not hard to see by UIP of Schatten norms that

where the right hand side is minimized only when  is diagonal. The last assertion comes from the facts that for any matrix
is diagonal. The last assertion comes from the facts that for any matrix 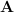 decomposed into its diagonal and off-diagonal elements,
decomposed into its diagonal and off-diagonal elements,  , we have
, we have  (generalized from Lemma 13 in this paper; also known in quantum information theory as (a particular case of) the pinching equality — see this slides) and
(generalized from Lemma 13 in this paper; also known in quantum information theory as (a particular case of) the pinching equality — see this slides) and  ,
, where the equality holds only when 
(the statement is wrong, there are counter-examples! Consider  for example). So the problem to solve reduces to seeking
for example). So the problem to solve reduces to seeking  (solved by simple component-wise arguments similar to that of soft-thresholding for the Lasso problem), upon which the optimal variable is
(solved by simple component-wise arguments similar to that of soft-thresholding for the Lasso problem), upon which the optimal variable is  .
.
2) On top of the above, the key is to verify  for orthogonal
for orthogonal  (convention here: “orthogonal” means
(convention here: “orthogonal” means  ), for which both directions are easy by the definition of positive semi-definiteness.
), for which both directions are easy by the definition of positive semi-definiteness.
3)Observing that  for symmetric
for symmetric  (implied from
(implied from  ), one can easily verify that
), one can easily verify that  . So the objective is equivalent to
. So the objective is equivalent to  .
. 
As mentioned, the above results are critical to devising proximal point kind of numerical algorithms (and also alternating direction method) for a large family of optimization problems involving the nuclear norm. Recently this paper working on subspace segmentation has a nice take into this slightly more “interesting” version of closed form solution (though the authors have failed to verified the uniqueness of the solution before they used the term “the optimal solution”, also their proof is by construction — less favorable to us as discussed).
Theorem 5 The optimal solution to the unconstrained optimization

is

where  is the SVD of
is the SVD of  and we have assumed
and we have assumed  and
and  for convenience. Furthermore
for convenience. Furthermore  .
.
Before moving into the actual proof, we note that the form of  is reminiscent of the solution to (2) and (3). Indeed the optimization problems are closely related — the difference lies at if the equality
is reminiscent of the solution to (2) and (3). Indeed the optimization problems are closely related — the difference lies at if the equality  is enforced through a constraint or a soft loss term. Besides though
is enforced through a constraint or a soft loss term. Besides though  are strictly convex w.r.t.
are strictly convex w.r.t.  , we can only show that
, we can only show that  is convex w.r.t.
is convex w.r.t.  as follows. For
as follows. For  , we have
, we have

where the last inequality follows from the observation that  ,
,

and  denotes matrix inner product. Notice that for the last inequality, the equality holds only when
denotes matrix inner product. Notice that for the last inequality, the equality holds only when  , or back to our complex form,
, or back to our complex form,  . On the other hand, for the inner product to norm product inequality in line 3 to 4, obviously the equality is taken only when
. On the other hand, for the inner product to norm product inequality in line 3 to 4, obviously the equality is taken only when  for a non-zero constant
for a non-zero constant 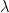 or any taking
or any taking  . Altogether, the equality is achieved only when
. Altogether, the equality is achieved only when  . This provides an important hint on when
. This provides an important hint on when  is strictly convex:
is strictly convex:
Proposition 6 For a given matrix  , if
, if  ,
,  is strictly convex. In other words,
is strictly convex. In other words,  is strictly convex when
is strictly convex when  is injective, or equivalently
is injective, or equivalently  has full column rank.
has full column rank.
So far it’s clear that the objective in (11) is in general not strictly convex, and hence the optimization may not yield unique minimizer. The following deferred proof shows otherwise positive.
Proof: , sketch} We assume the full SVD of  as
as  , implying
, implying  and
and  . By the UIP of Schattern norms, it’s easy to see
. By the UIP of Schattern norms, it’s easy to see  , and hence the objective can be written as
, and hence the objective can be written as  with the substitution
with the substitution  . For the diagonal (but non-vanishing)
. For the diagonal (but non-vanishing)  and a positive
and a positive  , it’s not hard to see that
, it’s not hard to see that  is minimized only when
is minimized only when 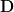 is also diagonal (by the pinching equality for nuclear norm as mentioned above and also property for squared Frobenius norm). The diagonal elements can be uniquely determined from the corresponding scalar optimization problems. For invertible
is also diagonal (by the pinching equality for nuclear norm as mentioned above and also property for squared Frobenius norm). The diagonal elements can be uniquely determined from the corresponding scalar optimization problems. For invertible 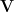 , we must have
, we must have  . The positive semi-definiteness can be easily established as the diagonal matrix
. The positive semi-definiteness can be easily established as the diagonal matrix  , i.e., is component-wise nonnegative.
, i.e., is component-wise nonnegative.
Uniqueness. The uniqueness can be seen from two different aspects.First, perhaps the most simple, we notice that the only source of ambiguity for  comes from the non-uniqueness of
comes from the non-uniqueness of 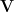 in the SVD. But we know from the above argument that the minimizer(s) has the form
in the SVD. But we know from the above argument that the minimizer(s) has the form  (for clarity, we switch to
(for clarity, we switch to  for a general orthogonal matrix). The form of
for a general orthogonal matrix). The form of  indicates that only those singular vectors corresponding to singular values that are greater than
indicates that only those singular vectors corresponding to singular values that are greater than  matter, i.e.,
matter, i.e.,  , where we have partitioned the matrices according to the threshold. However we must have
, where we have partitioned the matrices according to the threshold. However we must have  for a certain rotation matrix
for a certain rotation matrix  that represents the in-plane rotation of the subspace basis
that represents the in-plane rotation of the subspace basis  and
and  . The second way goes as follows. Suppose there is another minimizer in the form
. The second way goes as follows. Suppose there is another minimizer in the form  , we must have the perturbation relationship
, we must have the perturbation relationship  . It follows
. It follows

by which we conclude  .
. 
The above proof has verified Lemma 1 in this paper. Lemma 2 and 3 therein are built on the results of Lemma 1, and the uniqueness of the respective solution can also be established by similar perturbation argument as shown above.
— 3. Connection to other work and generalization —
Recently unitarily invariant norms used as regularizers in machine learning have been touched on in Ref [2]. This paper has in particular focused on characterize optimal solutions to such spectral regularization problems. In addition, Ref [1] shares similar flavors and talks about unitarily invariant functions as well . These techniques draws heavily from matrix analysis, and hence the seminal paper Ref [3] proves to be extremely useful here. Besides, the very fresh monograph Ref [4] on matrix-valued functions are also pertinent in this line (e.g., refer to this paperto see how some recent matrix cone programming are tackled).

— Further readings (References) —
- Lu, Z.S. and Zhang, Y. Penalty Decomposition Methods for Rank Minimization. Submitted to arXiv.org.
- Argyriou, A., Micchelli, C., Pontil, M. On Spectral Learning. Journal of machine learning research, 11(Feb):935 — 953, 2010
- Lewis, AS. The Convex Analysis of Unitarily Invariant Matrix Functions. Journal of Convex Analysis, 1995.
- Higham, Nick. Matrix Functions: Theory and Algorithms. Cambridge university press, 2008.
[Update Aug 12 2011] Refer to this paper also for similar discussions. (Citation: Yu, YL and Schuurmans. Rank/Norm Regularization with Closed-Form Solutions: Application to Subspace Clustering. In UAI 2011).
[Update Jan 25 2012] I repeatedly encountered situations where variational characterization of nuclear norm could be useful. One piece of result, for example, is  (this can be found in this paper without proof). To see this is true, one can set
(this can be found in this paper without proof). To see this is true, one can set  and
and  where
where  is the SVD of
is the SVD of  , suggesting
, suggesting  . On the other hand, the Cauchy-Schwarz inequality for unitarily invariant norms tells
. On the other hand, the Cauchy-Schwarz inequality for unitarily invariant norms tells  (see, e.g., Ex IV 2.7 in Matrix Analysis by Bhatia).
(see, e.g., Ex IV 2.7 in Matrix Analysis by Bhatia).






